k-Nearest Neighbors#
k-Nearest Neighbors (kNN) is a supervised machine learning algorithm used for both classification and regression tasks. It is considered a “lazy learner” because it does not build a model during training. Instead, it memorizes the training data and uses it directly for predictions.
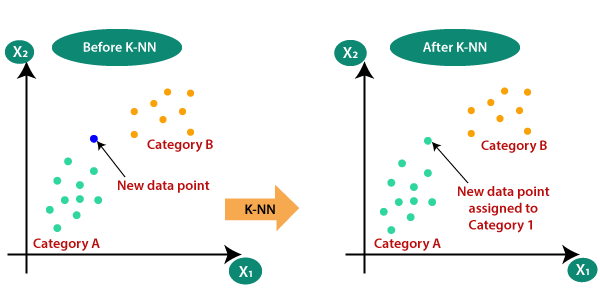
kNN for classification#
In classification problems kNN stores all the labeled training data points. Each data point has features (its attributes) and a class label (what it represents).
When a new unlabeled data point is provided to be classified the algorithm does the following:
Measures the distance between the new data point and all the stored data points. Common distance measures include Euclidean distance (straight-line distance), Manhattan distance (city block distance), or others.
Selects the \(k\) closest data points (neighbors) to the new data point. The \(k\) value is a model hyperparameter.
Examines the class labels of the \(k\) nearest neighbors. If using a majority vote, the most frequent class label among the neighbors becomes the predicted class for the new data point. If using a weighted vote, closer neighbors have more influence on the prediction.
kNN for regression#
The process is similar, but instead of taking a majority or weighted vote, the kNN algorithm calculates the average (or weighted average) of the target values of the \(k\) nearest neighbors. This average becomes the predicted value for the new data point.
Selection of the k value#
The number of neighbors, \(k\), is a model hyperparameter. The best \(k\) can be chosen using techniques like cross-validation.
Small \(k\) (e.g., \(k=1\)): The model is more sensitive to noise and outliers, potentially leading to overfitting.
Large \(k\) (e.g., \(k=10\)): The model becomes less flexible and might underfit the data.
Strengths of kNN#
Is simple to understand and implement.
No model needs to be trained.
Can be used for both classification and regression.
Works well for non-linear data distributions.
Weaknesses of kNN#
Calculating distances for every new data point can be slow for large datasets.
Features with larger scales can dominate the distance calculations. It’s crucial to normalize or standardize your features.
kNN performance can degrade in high-dimensional spaces due to the increasing sparsity of data (Curse of Dimensionality).
