Linear models

Fitting a function \(f(.)\) to datapoints \(y_i=f(x_i)\) under some error function. Based on the estimated function and error, we have the following types of regression.

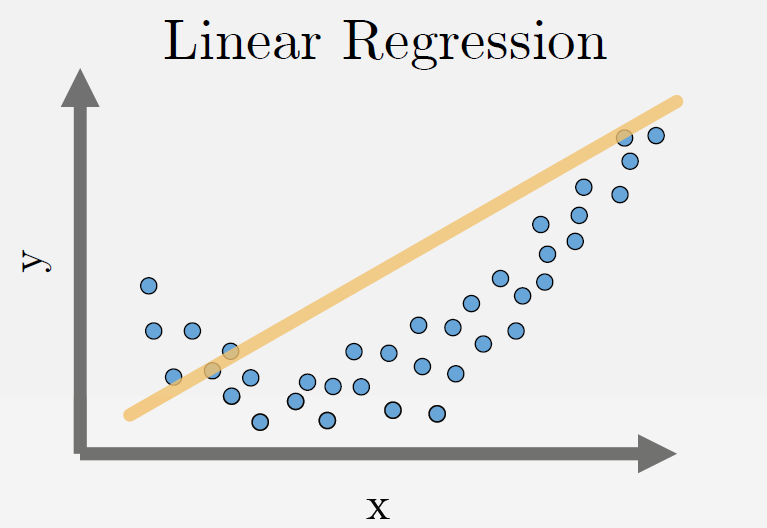
Linear Regression

Fits a line minimizing the sum of mean-squared error for each datapoint.

\[min_{\beta} \sum_{i} (y_i - f_{\beta}^{linear})^2\]

\[f_{\beta}^{linear}(x_i) = \beta_0 + \beta_1 x_i\]

• Linear regression
• Fit a simple linear regression to 2D data
• Multilinear regression
• Adapting linear regression to nonlinear relationships

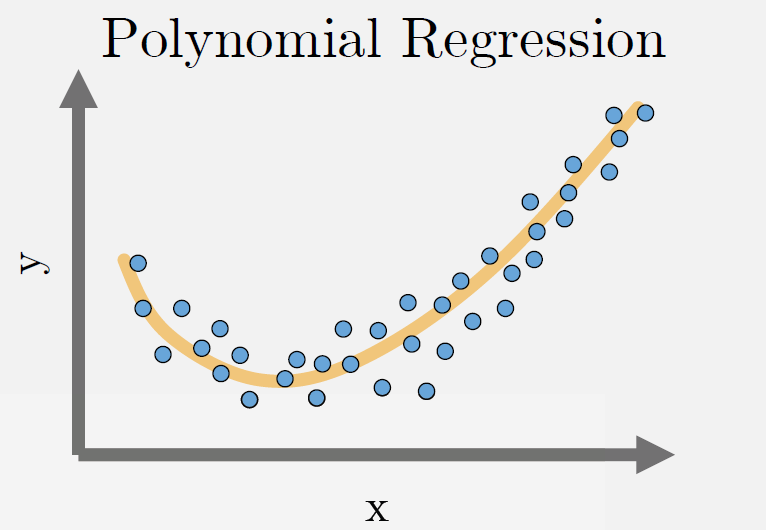
Polynomial Regression

Fits a polynomial of order \(k\) (\(k+1\) unknowns) minimizing the sum of mean-squared error for each datapoint.

\[min_{\beta} \sum_{i} (y_i - f_{\beta}^{poly})^2\]

\[f_{\beta}^{poly}(x_i) = \beta_0 + \beta_1 x_i + \beta_2 x_i^2 + ... + \beta_k x_i^k\]

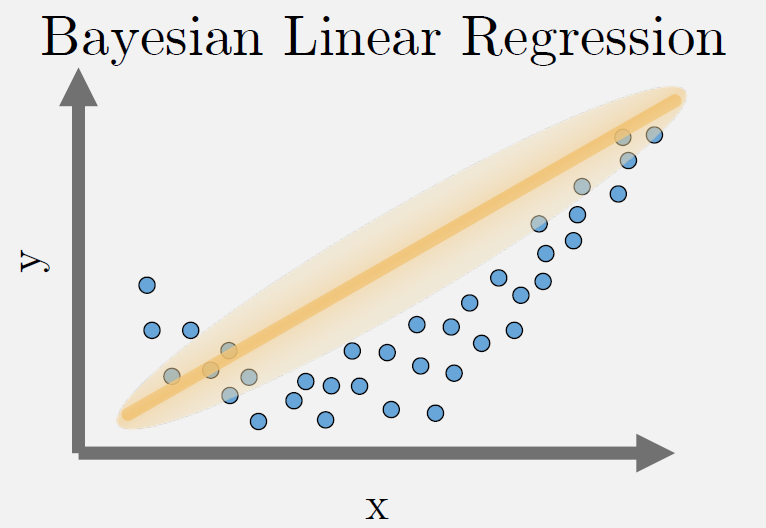
Bayesian Regression

For each datapoint, fits a gaussian distribution by minimizing the mean-squared error. As the number of data points xi increases, it converges to point estimates i.e. \(n \rightarrow \infty, \sigma^2 \rightarrow 0\)

\[min_{\beta} \sum_{i} [y_i - \mathcal{N}(f_{\beta}(x_i), \sigma^2)]^2\]

where \(\mathcal{N}(\mu, \sigma^2)\) is a Gaussian distribution with mean \(\mu\) and variance \(\sigma^2\)

\[f_{\beta}(x_i) = f_{\beta}^{linear}(x_i) \quad \mathrm{or} \quad f_{\beta}^{poly}(x_i)\]

Ridge Regression

Can fit either a line, or polynomial minimizing the sum of mean-squared error for each datapoint and the weighted L2 norm of the function parameters beta.

LASSO Regression

Can fit either a line, or polynomial minimizing the the sum of mean-squared error for each datapoint and the weighted L1 norm of the function parameters beta.

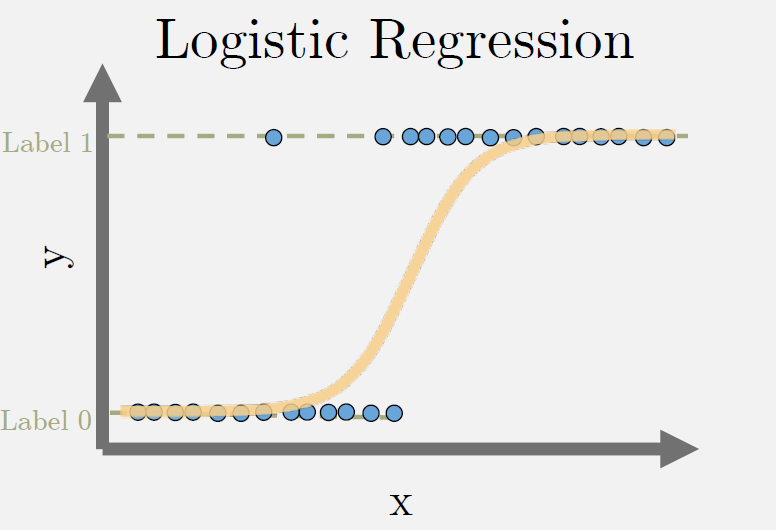
Logistic Regression

Can fit either a line, or polynomial with sigmoid activation minimizing the binary cross-entropy loss for each datapoint. The labels y are binary class labels.