Machine Learning Basics#
Features#
In machine learning, features are also referred to as variables, predictors, attributes, inputs, or independent variables. All these terms refer to the input variables or attributes that are used to train a machine learning model and make predictions. They are the measurable characteristics or properties of the data that can be used to predict the output or target variable. The choice of features is a critical step in the machine learning process, as the quality and relevance of the features can greatly impact the accuracy and performance of the model.
Target#
The target variable is the variable that the model is trying to predict. It is also known as the dependent variable, response variable, outcome variable, output variable or label. This later term (“label”) is often used in classification tasks, where the target variable is a categorical variable that is used to label or classify instances of data. The target variable is the variable that is affected by changes in the input variables, or features.
For example, in a model that predicts house prices, the target variable would be the house price, and the features would be various attributes of the house such as its size, number of bedrooms, location, etc. The model would take in these features as inputs and output a predicted house price.
Hyperparameters#
Hyperparameters are parameters that are not learned directly from the training data, but must be set by the user before the learning process begins. These parameters define the characteristics of a machine learning model and affect its learning process.
Hyperparameters are usually set through trial and error, intuition, or by using techniques like grid search or random search. The optimal values of hyperparameters may vary depending on the specific problem, dataset, and model architecture. Finding the right hyperparameters often requires experimentation and fine-tuning to achieve the best performance.
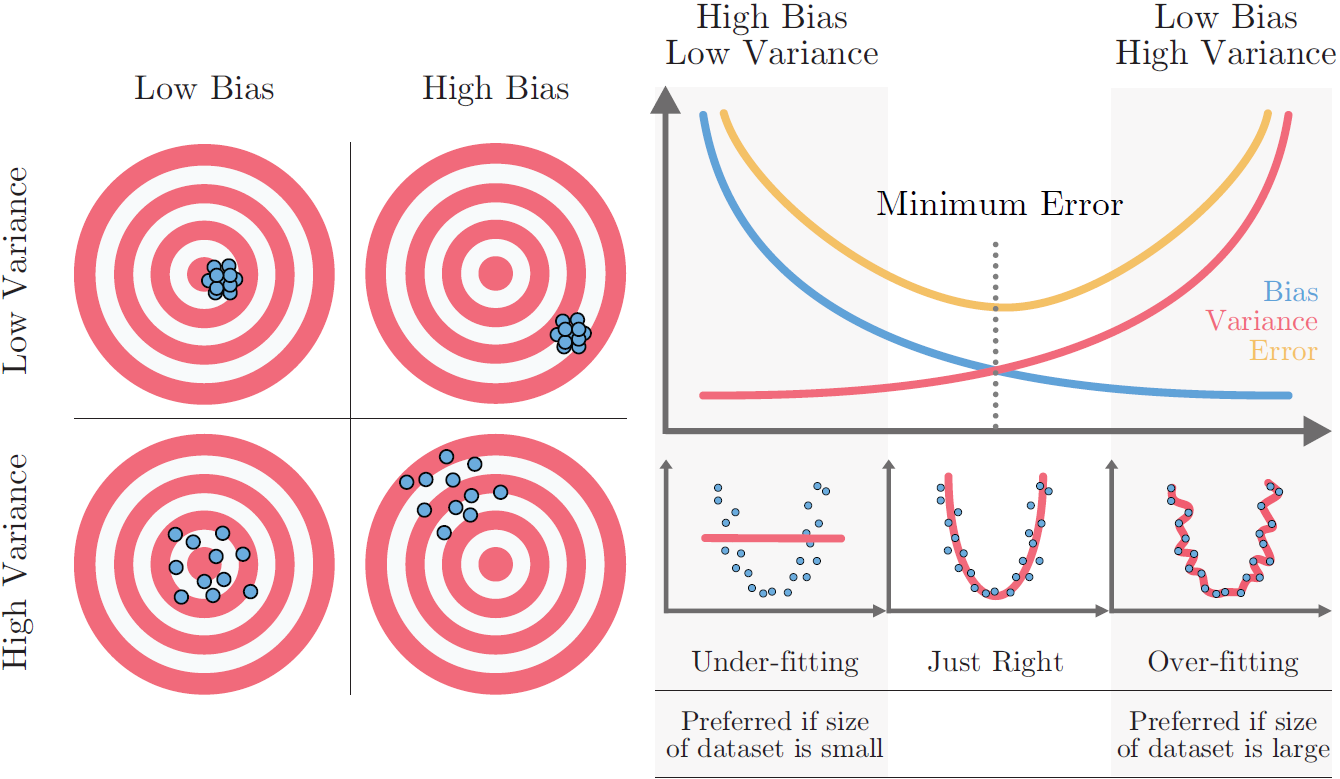
Bias-Variance Tradeoff#
What is bias?
Error between average model prediction and ground truth.
The bias of the estimated function tells us the capacity of the underlying model to predict the values.
High bias might mean:
Overly-simplified Model
Under-fitting
High error on both test and train data
What is variance?
Average variability in the model prediction for the given dataset.
The variance of the estimated function tells you how much the function can adjust to the change in the dataset.
High variance might mean:
Overly-complex Model
Over-fitting
Low error on train data and high on test
Starts modelling the noise in the input
Bias-variance Trade-off:
Increasing bias (not always) reduces variance and vice-versa
Error = bias^2 + variance + irreducible error
The best model is where the error is reduced.
Compromise between bias and variance